مدل بازاریابان حرفه‌ای

شکل بالا مراحل اولیه رشد درخت بازاریابی شبکه ای را نشان می‌دهد. در مرحله اول رأس درخت اولین مشتری را پیدا می‌کند. در ادامه، نه تنها رأس بالایی به دنبال مشتری دوم خود می‌گردد، بلکه مشتری قبلی نیز در جستجوی اولین طعمه خود است. لذا در مرحله دوم، دو نفر جدید، همان طور که در شکل می‌بینید، به درخت اضافه می‌شوند. اکنون اولین فرد دو بازوی خود را تکمیل کرده است و دیگر از طریق وی کسی به درخت اضافه نمی‌شود و لذا در این درخت ۴ رأسه، سه نفر به دنبال مشتری هستند و در نتیجه در مرحله بعد درخت ما ۷ رأس خواهد داشت.
اگر تا چند مرحله دیگر رشد درخت را بررسی کنید می‌بینید که تعداد افراد آلوده در مراحل مختلف به این صورت است.
۱، ۲، ۴، ۷، ۱۲، ۲۰، ۳۳، ۵۴، ...
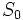برای بررسی دقیق‌تر درخت مورد بحث تعداد رأس‌ها در مرحله را می‌نامیم. در این صورت برابر ۱، و 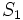برابر ۲ است. با اندکی توجه می‌توان رابطه‌ای بازگشتی برای این دنباله به دست آورد؛ دو مشتری‌ای که توسط نفر اول وارد بازی شده‌اند یکی یک مرحله و دیگری دو مرحله از رأس اولی عقب‌ترند، و لذا درختی که در مرحله n ام زیر آن دو تشکیل می‌شود دقیقاً مشابه درخت اصلی در یک مرحله پیش و درخت اصلی در دو مرحله پیش است. نتیجه این که در مرحله n ام در بازوی راست رأس بالایی 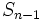نفر و در بازوی چپ 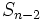نفر قرار دارد. اگر رأس بالایی را هم در نظر بگیریم رابطه بازگشتی زیر به دست می‌آید.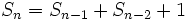

به کمک این رابطه می‌توانیم تعداد اعضای درخت بازاریابی شبکه ای را به دست آوریم. اگر دو طرف تساوی اخیر را با یک جمع کنیم و به علاوه (۱ + ) را 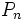بنامیم، به رابطه زیر می‌رسیم: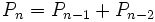

اگر با دنباله معروف فیبوناتچی آشنا باشید می‌دانید که در آن‌جا نیز هر جمله دنباله برابر جمع دو جمله قبلی است. تفاوت دنباله Pn و دنباله فیبوناتچی ناشی از تفاوت در دو جمله اول است؛ ۰P برابر ۲، و ۱P برابر ۳ است، در حالی که ۰F و ۱F هر دو برابر ۱ اند. پس آیا ارتباطی بین جمله‌های دنباله Pn و جمله‌های دنباله فیبوناتچی وجود ندارد؟ اجازه دهید نگاهی به چند جمله اول هر دو دنباله بیندازیم.
۸ ۷ ۶ ۵ ۴ ۳ ۲ ۱ ۰ n
۸۹ ۵۵ ۳۴ ۲۱ ۱۳ ۸ ۵ ۳ ۲ Pn
۳۴ ۲۱ ۱۳ ۸ ۵ ۳ ۲ ۱ ۱ Fn
اکنون به سادگی می‌توان دید که Pn در واقع همان دنباله فیبوناتچی است که دو جمله اول آن حذف شده است، یعنی
Pn = Fn+۲
و در نتیجه
Sn = Fn+۲ - ۱
تا این‌جا توانستیم تعداد افراد آلوده در مرحله n را به دست آوریم. اکنون سؤال این است که در هر مرحله وضعیت تعادل افراد (یعنی مینیمم تعداد زیردست‌های راست و تعداد زیردست‌های چپ) چگونه است؟
جواب این سؤال در مورد شروع‌کننده درخت تلویحاً داده شده است. دو بازوی این فرد شامل ۱Sn- نفر و ۲Sn- نفر است و در نتیجه تعادلش ۲Sn- است که طبق محاسبات انجام شده برابر است با ۱ - Fn.
با توجه به این که هر عضو دیگر درخت نیز وضعیتی شبیه نفر اول در چند مرحله قبل دارد، تعادل وی نیز به شکل ۱ – Fk است که در آن k برابر تعداد مراحلی است که پس از اتصال وی به درخت طی شده است. حال می‌خواهیم بفهمیم در مرحله n ام چند نفر چنین تعادلی دارند؟
در لحظه ورودِ آن عضو نوعی، n – k مرحله درخت رشد کرده است و در نتیجه، در آن مقطع، تعداد افراد آلوده از Sn-k-۱ به Sn-k رسیده است و لذا Sn-k-۱ - Sn-k نفر به درخت اضافه شده‌اند. با در نظر گرفتن مطالب بالا این مقدار برابر است با
(Fn-k+۲ - ۱) - (Fn-k+۱ - ۱)
و به عبارت دیگر Fn-k.
پس تا اینجا نشان دادیم که در مدل ارایه شده در مرحله n ام Fn-k نفر تعادلشان برابر ۱ – Fk است. البته عبارت اخیر در یک مورد درست نیست؛ به این نکته توجه کنید که تعادل هر فرد در ابتدای ورود به بازی و هم‌چنین پس از گذشت یک مرحله صفر است (F۰ - ۱ = F۱ - ۱ = ۰) و لذا تعداد کسانی که تعادلشان صفر است برابر است با Fn + Fn-۱ که همان Fn+۱ است. در مراحل بعدی، پس از گذشت هر مرحله، تعادل افزایش پیدا خواهد کرد. در نتیجه عبارت مورد بحث برای k های بزرگ‌تر از یک، صادق است.
به بیان دیگر در مرحله n ام نسبت کسانی که تعادلشان صفر است برابر است با
(Fn+۲ - ۱)/ Fn+۱
و نسبت کسانی که تعادلشان ۱ – Fk است (۱ < k)، برابر است با
(Fn+۲ - ۱)/ Fn-k
این نسبت‌ها هنوز توصیف روشنی از وضعیت بازی ارایه نمی‌کنند. گزاره زیر به ما کمک خواهد کرد که به مدل مورد بحث را بهتر تحلیل کنیم.
گزاره: وقتی n به بی‌نهایت میل کند، Fn/ Fn+۱ به φمیل می‌کند که φ، "عدد طلایی"، یعنی ریشه مثبت معادله درجه دو زیر است.
φ۲ – φ – ۱ = ۰
۶۲ ۱/ ۵)/۲ ۱+) = φ
اثبات این گزاره چندان مشکل نیست. اگر هم ایده‌ای برای اثباتش ندارید بد نیست نسبت جمله‌های متوالی دنباله فیبوناتچی را محاسبه کنید و "ببینید" که آیا به φ میل می‌کند یا خیر!
گزاره مذکور نتیجه‌ای دارد که به کار می‌آید.
نتیجه: برای هر k، وقتی n به بی‌نهایت میل کند، Fn/ Fn+k به φKمیل می‌کند.
برای اثبات این موضوع کافی است توجه کنید که کسر مذکور با عبارت زیر برابر است.
Fn/ Fn+۱ … F n+k-۲ / Fn+k-۱ Fn+k-۱/ Fn+k
اکنون می‌توانیم توصیف بهتری از وضعیت مشتریان بازاریابی شبکه ای ارایه دهیم. برای n های به اندازه کافی بزرگ، φ-۱ نسبت افرادی است که تعادلشان صفر است و نسبت کسانی که تعادلشان ۱ – Fk است (۱ < k)، برابر است با φ-K-۲. جدول زیر که در آن از مقدار تقریبی φ استفاده شده است گویاتر است.
تعادل نسبت افرادی که تعادلشان برابر این مقدار است نسبت افرادی که تعادلشان کم‌تر یا مساوی این مقدار است
0 68.1درصد 68.1درصد
1 14.6درصد 76.4درصد
2 9.0درصد 85.4درصد
4 5.6درصد 91.0درصد
7 3.4درصد 94.4درصد
12 2.1درصد 96.6درصد
20 1.3درصد 97.9درصد
33 0.8درصد 98.7درصد
54 0.5درصد 99.2درصد
88 0.3درصد 99.5درصد
143 0.2درصد 99.7درصد
232 0.1درصد 99.8درصد
اولین پورسانت هنگامی داده می‌شود که تعادل فرد به 3 برسد. پس طبق محاسبات انجام شده همیشه در حدود ۵/۴۸ درصد از کسانی که وارد این بازی شده‌اند هیچ پورسانتی دریافت نکرده‌اند!
در این حالت که درخت اعضاء کم و بیش منظم رشد کند. با توجه به پیچیدگی محاسبات تحلیلی، باید به سراغ شبیه‌سازی کامپیوتری رفت.نتایج حاصل از یک شبیه‌سازی نسبتاً خوب، در زیر آمده است:
کسانی که 560 دلار ضرر کرده‌اند تقریباً 6/66 درصد
کسانی که 510 دلار ضرر کرده‌اند تقریباً 4/17 درصد
کسانی که 260 دلار ضرر کرده‌اند تقریباً 7/7 درصد
کسانی که 10 دلار ضرر کرده‌اند تقریباً 6/2
کسانی که سود کرده‌اند تقریباً 7/5
در این حالت هر مال‌باخته، به طور متوسط، بیش از 9/481 دلار از دست داده است و در مجموع بیش از 240 میلیون دلار وارد جیب کلاه‌برداران شده است!
البته توجه کنید که این اعداد و ارقام در حالتی به دست آمد که درخت افراد آلوده کاملاً منظم رشد کرد. در حالت واقعی، که رشد درخت منظم نیست، وضع بسیار وخیم‌تر از این خواهد شد.